Class Ix Rs Aggarwal All Chapter

RS Aggarwal Chapter 1 Class 9 Maths Exercise 1.6 Solutions: Number System is the essential study material for students preparing for the CBSE exam. “Number system” is the most important subject in mathematics because it also forms the basis of other chapters in mathematics. RS Aggarwal Maths Solutions Class 9 Chapter 1 has 7 exercises and has problems that give you complete knowledge about types of numbers, ie. Real, natural, rational / irrational, imaginary, integer, prime and numbers respectively, their representation on number line, rationalization and exponential rules, etc.

Exercise 1F consists of 25 questions based on the denominator rationalization factor.

Download RS Aggarwal Chapter 1 Class 9 Maths Exercise 1.6 Solutions

R S Aggarwal and V Aggarwal Solutions for Class 9 Mathematics CBSE, 14 Areas of Triangles and Quadrilaterals. All the solutions of Areas of Triangles and Quadrilaterals - Mathematics explained in detail by experts to help students prepare for their CBSE exams. All questions and answers from the Rs Aggarwal 2019 2020 Book of Class 9 Math Chapter 2 are provided here for you for free. You will also love the ad-free experience on Meritnation’s Rs Aggarwal 2019 2020 Solutions. All Rs Aggarwal 2019 2020 Solutions for class Class 9 Math are prepared by experts and are 100% accurate.

Important Definition for RS Aggarwal Chapter 11 Class 9 Maths Ex 1f Solutions

RS Aggarwal Class 9 Maths Solutions Chapter 12 is designed in such a manner that it will help you solve the RS Aggarwal problems with ease. Revising the chapter from this book will enable you to practice the questions all the more effectively.
See also: rs aggarwal maths book class 9 pdf free download rs aggarwal maths book class 9 pdf free download 2018 rs aggarwal maths book class 9 solutions pdf free download analysis for marketing planning lehmann 7th edition manual de uso microondas galanz libro de buen amor pdf todas las playas de mallorca 262 perlas por descubrir pdf sinopsis de psiquiatria kaplan 10.
RS Aggarwal Maths Book Solutions – All Chapters and Exercises RS Aggarwal Solutions for class 6 to 12 is made available for free PDF download by our subject experts. It helps to promote an in-depth understanding of concepts in a very simplistic and precise manner.

Introduction to natural numbers-

The Set of positive counting numbers excluding zero are natural numbers.

Whole numbers –

The Set of positive counting numbers including zero are whole numbers

Integers – Integers has two types-

Positive integers – Set of all natural numbers including zero is positive integers.

Negative integers – Set of all non-positive counting numbers including zero is negative integers.

Rational Numbers-

Rational numbers are those types of numbers which are represented in the form of (P/Q) where Q does not equal to zero

How to find a rational number between two numbers

If ‘a’ and ‘b’ are the two numbers-

Rational no.= (a+b)/2

Irrational numbers –

A number that is not represented in the form of (P/Q) are irrational numbers.

Real numbers –

Real numbers include all numbers which are rational or irrational.

Prime numbers-

A number which is divided by number 1 and by itself are called prime numbers.

Composite numbers- A composite number, is a positive integer or whole number that can be formed by the multiplication of two whole numbers.
Complex numbers –

Complex numbers are those types of numbers that contain real as well as imaginary numbers.

Laws of Exponent –

If a and b are the two numbers and m,n are the exponents –

am× an = am+n
(am)n= amn
ambm = (ab)m
a0= 1
a1= a
1/an= a-n

Rationalizing the denominator–

If the denominator contains a surd, then multiplying both by numerator and denominator by the surd is termed as rationalizing a denominator.

Know more at the Official Website.

Rs Aggarwal 2019 2020 Solutions for Class 9 Math Chapter 5 Coordinate Geometry are provided here with simple step-by-step explanations. These solutions for Coordinate Geometry are extremely popular among Class 9 students for Math Coordinate Geometry Solutions come handy for quickly completing your homework and preparing for exams. All questions and answers from the Rs Aggarwal 2019 2020 Book of Class 9 Math Chapter 5 are provided here for you for free. You will also love the ad-free experience on Meritnation’s Rs Aggarwal 2019 2020 Solutions. All Rs Aggarwal 2019 2020 Solutions for class Class 9 Math are prepared by experts and are 100% accurate.

Page No 174:

Question 1:

On the plane of a graph paper draw X'OX and YOY' as coordinate axes and plot each of the following points.
(i) A(5, 3)
(ii) B(6, 2)
(iii) C(–5, 3)
(iv) D(4, –6)
(v) E(–3, –2)
(vi) F(–4, 4)
(vii) G(3, –4)
(viii) H(5, 0)
(ix) I(0, 6)
(x) J(–3, 0)
(xi) K(0, –2)
(xii) O(0, 0)

Answer:

(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
(viii)
(ix)
(x)
(xi)
(xii)

Page No 175:

Question 2:

Write down the coordinates of each of the points A, B, C, D, E shown below:

Answer:

Draw perpendicular AL, BM, CN, DP and EQ on the X-axis.
(i) Distance of A from the Y-axis = OL = -6 units
Distance of A from the X-axis = AL = 5 units
Hence, the coordinates of A are (-6,5).
(ii) Distance of B from the Y-axis = OM = 5 units
Distance of B from the X-axis = BM = 4 units
Hence, the coordinates of B are (5,4).
(iii) Distance of C from the Y-axis = ON = -3 units
Distance of C from the X-axis = CN = 2 units
Hence, the coordinates of C are (-3,2).
(iv) Distance of D from the Y-axis = OP = 2 units
Distance of D from the X-axis = DP = -2 units
Hence, the coordinates of D are (2,-2).
(v) Distance of E from the Y-axis = OL = -1 units
Distance of E from the X-axis = AL = -4 units
Hence, the coordinates of E are (-1,-4).

Page No 175:

Question 3:

For each of the following points, write the quadrant in which it lies
(i) (–6, 3)
(ii) (–5, –3)
(iii)(11, 6)
(iv) (1, –4)
(v) (–7, –4)
(vi) (4, –1)
(vii) (–3, 8)
(viii) (3, –8)

Answer:

(i) (–6, 3)
Points of the type (–, +) lie in the II quadrant.
Hence, the point lies (–6, 3) in the II quadrant.
(ii) (–5, –3)
Points of the type (–, –) lie in the III quadrant.
Hence, the point lies (–5, –3) in the III quadrant.
(iii)(11, 6)
Points of the type (+, +) lie in the I quadrant.
Hence, the point lies (11, 6) in the I quadrant.
(iv) (1, –4)
Points of the type (+, –) lie in the IV quadrant.
Hence, the point lies (1, –4) in the IV quadrant.
(v) (–7, –4)
Points of the type (–, –) lie in the III quadrant.
Hence, the point lies (–7, –4) in the III quadrant.
(vi) (4, –1)
Points of the type (+, –) lie in the IV quadrant.
Hence, the point lies (4, –1) in the IV quadrant.
(vii) (–3, 8)
Points of the type (–, +) lie in the II quadrant.
Hence, the point lies (–3, 8) in the II quadrant.
(viii) (3, –8)
Points of the type (+, –) lie in the IV quadrant.
Hence, the point lies (3, –8) in the IV quadrant.

Page No 175:

Question 4:

Write the axis on which the given point lies.
(i) (2, 0)
(ii) (0, –5)
(iii) (–4, 0)
(iv) (0, –1)

Answer:

(i) (2, 0)
The ordinate of the point (2, 0) is zero.
Hence, the (2, 0) lies on the x-axis.
(ii) (0, –5)
The abscissa of the point (0, –5) is zero.
Hence, the (0, –5) lies on the y-axis.
(iii) (–4, 0)
The ordinate of the point (–4, 0) is zero.
Hence, the (–4, 0) lies on the x-axis.
(iv) (0, –1)
The abscissa of the point (0, –1) is zero.
Hence, the (0, –1) lies on the y-axis.

Page No 175:

Question 5:

Which of the following points lie on the x-axis?
(i) A(0, 8)
(ii) B(4, 0)
(iii) C(0, –3)
(iv) D(–6, 0)
(v) E(2, 1)
(vi) F(–2, –1)
(vii) G(–1, 0)
(viii) H(0, –2)

Answer:

(i) A(0, 8)
The given point does not lies on the x-axis.
(ii) B(4, 0)
The ordinate of the point (4, 0) is zero.
Hence, the (4, 0) lies on the x-axis.
(iii) C(0, –3)
The given point does not lies on the x-axis.
(iv) D(–6, 0)
The ordinate of the point (–6, 0) is zero.
Hence, the (–6, 0) lies on the x-axis.
(v) E(2, 1)
The given point does not lies on the x-axis.
(vi) F(–2, –1)
The given point does not lies on the x-axis.
(vii) G(–1, 0)
The ordinate of the point (–1, 0) is zero.
Hence, the (–1, 0) lies on the x-axis.
(viii) H(0, –2)
The given point does not lies on the x-axis.

Page No 175:

Question 6:

Plot the points A(2, 5), B(–2, 2) and C(4, 2) on a graph paper. Join AB, BC and AC. Calculate the area of ∆ABC.

Answer:

Abscissa of D = Abscissa of A = 2
Ordinate of D = Ordinate of B = 2
Now,
BC = (2 + 4) units = 6 units
AD = (5 – 2) units = 3 units
$Area of ∆ A B C = \frac{1}{2} \times Base \times Height = \frac{1}{2} \times B C \times A D = \frac{1}{2} \times 6 \times 3 = 9$
Hence, area of ∆ABC is 9 square units.

Page No 175:

Question 7:

Three vertices of a rectangle ABCD are A(3, 1), B(–3, 1) and C(–3, 3). Plot these points on a graph paper and find the coordinates of the fourth vertex D. Also, find the area of rectangle ABCD.

Answer:

Let A(3, 1), B(–3, 1) and C(–3, 3) be three vertices of a rectangle ABCD.
Let the y-axis cut the rectangle ABCD at the points P and Q respectively.
Abscissa of D = Abscissa of A = 3.
Ordinate of D = Ordinate of C = 3.
∴ coordinates of D are (3, 3).
AB = (BP + PA) = (3 + 3) units = 6 units.
BC = (OQ – OP) = (3 – 1) units = 2 units.
Ar(rectangle ABCD) = (AB × BC)
= (6 × 2) sq. units
= 12 sq. units
Hence, the area of rectangle ABCD is 12 square units.

Page No 176:

Question 1:

In which quadrant does the point (–7, –4) lie?
(a) IV
(b) II
(c) III
(d) None of these

Answer:

Points of the type (–, –) lie in the III quadrant.
The point (–7, –4) lies in the III quadrant.
Hence, the correct option is (c).

Page No 176:

Question 2:

If x > 0 and y < 0, then the point (x, y) lies in
(a) I
(b) III
(c) II
(d) IV

Answer:

(d) IV
Explanation:
The points of the type (+,-) lie in fourth quadrant.
Hence, the point (x,y), where x > 0 and y < 0, lies in quadrant IV.

Page No 176:

Class 9 Rs Aggarwal Chapter 1

Question 3:

If a < 0 and b > 0, then the point (a, b) lies in quadrant
(a) IV
(b) II
(c) III
(d) none of these

Answer:

Ans (b)
Explanation:
Points of the type (-,+) lie in the second quadrant.
Hence, the point P(a,b), where a < 0 and b > 0, lie in quadrant II.

Page No 176:

Question 4:

A point both of whose coordinates are negative lies in
(a) quadrant I
(b) quadrant II
(c) quadrant III
(d) quadrant IV

Answer:

Page No 176:

Question 5:

The points (other than origin) for which abscissa is equal to the ordinate will lie in the quadrant
(a) I only
(b) I or II
(c) I or III
(d) II or IV

Answer:

(c) I or III
Explanation:
If abscissa = ordinate, there could be two possibilities.
Either both are positive or both are negative. So, a point could be either (+,+), which lie in quadrant I or it could be of the type (-,-), which lie in quadrant III.
Hence, the points (other then the origin) for which the abscissas are equal to the ordinates lie in quadrant I or III.

Page No 176:

Question 6:

The points (–5, 3) and (3, –5) lie in the
(a) same quadrant
(b) II and III quadrants respectively
(c) II and IV quadrants respectively
(d) IV and II quadrants respectively

Answer:

The point (–5, 3) lies in the II quadrant.
The point (3, –5) lies in the IV quadrant.
Hence, the correct option is (c).

Page No 176:

Question 7:

Points (1, –1), (2, –2), (–3, –4), (4, –5)
(a) all lie in the II quadrant
(b) all lie in the III quadrant
(c) all lie in the IV quadrant
(d) do not lie in the same quadrant

Answer:

The point (1, –1) lies in the IV quadrant.
The point (2, –2) lies in the IV quadrant.
The point (–3, –4) lies in the III quadrant.
The point (4, –5) lies in the IV quadrant.
Hence, the correct option is (d).

Page No 176:

Question 8:

Point (0, –8) lies
(a) in the II quadrant
(b) in the IV quadrant
(c) on the x-axis
(d) on the y-axis

Answer:

The abscissa of the point (0, –8) is zero.
The point (0, –8) lies on the y-axis.
Hence, the correct option is (d).

Page No 176:

Question 9:

Point (–7, 0) lies
(a) on the negative direction of the x-axis
(b) on the negative direction of the y-axis
(c) in the III quadrant
(d) in the IV quadrant

Answer:

The point (–7, 0) lies on the negative direction of the x-axis.
Hence, the correct option is (a).

Page No 177:

Question 10:

The point which lies on the y-axis at a distance of 5 units in the negative direction of the y-axis is
(a) (–5, 0)
(b) (0, –5)
(c) (5, 0)
(d) (0, 5)

Answer:

The point which lies on the y-axis at a distance of 5 units in the negative direction of the y-axis is (0, –5).
Hence, the correct option is (b).

Page No 177:

Question 11:

The ordinate of every point on the x-axis is
(a) 1
(b) –1
(c) 0
(d) any real number

Answer:

The ordinate of every point on the x-axis is 0.
Hence, the correct option is (c).

Page No 177:

Question 12:

If the y-coordinate of a point is zero then this point always lies
(a) on the y-axis
(b) on the x-axis
(c) in the I quadrant
(d) in the IV quadrant

Answer:

The coordinates of a point on the x-axis are of the form (x, 0) and that of the point on the y-axis is of the form (0, y).
Thus, if the y-coordinate of a point is zero, then this point always lies on the x-axis.
Hence, the correct answer is option (b).

Page No 177:

Question 13:

If O(0, 0), A(3, 0), B(3, 4), C(0, 4) are four given points then the figure OABC is a
(a) square
(b) rectangle
(c) trapezium
(d) rhombus

Answer:

Class 9 Rs Aggarwal Chapter 15

The point O(0, 0) is the origin.
A(3, 0) lies on the positive direction of x-axis.
B(3, 4) lies in the Ist quadrant.
C(0, 4) lies on the positive direction of y-axis.
The points O(0, 0), A(3, 0), B(3, 4) and C(0, 4) can be plotted on the Cartesian plane as follows:
Here, the figure OABC is a rectangle.
Hence, the correct answer is option (b).

Page No 177:

Question 14:

If A(–2, 3) and B(–3, 5) are two given points then (abscissa of A) – (abscissa of B) = ?
(a) –2
(b) 1
(c) –1
(d) 2

Answer:

The given points are A(–2, 3) and B(–3, 5).
Abscissa of A = x-coordinate of A = –2
Abscissa of B = x-coordinate of B = –3
∴ Abscissa of A – Abscissa of B = –2 – (–3) = –2 + 3 = 1
Hence, the correct answer is option (b).

Page No 177:

Question 15:

The perpendicular distance of the point A(3, 4) from the y-axis is
(a) 3
(b) 4
(c) 5
(d) 7

Answer:

The perpendicular distance of a point from the y-axis is equal to the x-coordinate of the point.
∴ Perpendicular distance of the point A(3, 4) from the y-axis = x-coordinate of A(3, 4) = 3
Hence, the correct answer is option (a).

Page No 177:

Question 16:

Abscissa of a point is positive in
(a) I and II quadrants
(b) I and IV quadrants
(c) I quadrant only
(d) II quadrant only

Answer:

$Chapter$

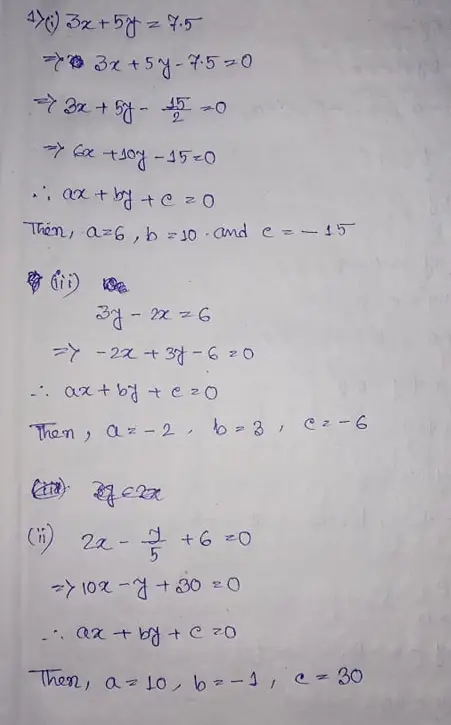
(b) I and IV quadrants
Explanation:
If abscissa of a point is positive, then the ordinate could be either positive or negative.
It means that the type of any point can be either (+,+) or (+, -).
Points of the type (+,+) lie in quadrant I, whereas points of the type (+,-) lie in quadrant IV.

Class Ix Rs Aggarwal All Chapter Book

Page No 177:

Question 17:

The point at which the two coordinate axes meet is called
(a) the abscissa
(b) the ordinate
(c) the origin
(d) the quadrant

Answer:

Class Ix Rs Aggarwal All Chapter 2

Page No 177:

Question 18:

The point whose ordinate is 3 and which lies on the y-axis is
(a) (3, 0)
(b) (0, 3)
(c) (3, 3)
(d) (1, 3)

Answer:

The ordinate of a point is the y-coordinate of the point. So, the y-coordinate of the point is 3.
Also, any point on the y-axis has coordinates in the form (0, y).
Thus, the point whose ordinate is 3 and which lies on the y-axis is (0, 3).
Hence, the correct answer is option (b).

Page No 177:

Question 19:

Which of the following points lies on the line y = 2x + 3?
(a) (2, 8)
(b) (3, 9)
(c) (4, 12)
(d) (5, 15)

Answer:

(b) (3,9)
Explanation:
Point (2,8) does not satisfy the equation y = 2x + 3. (∵ y = 2 × 2 + 8 = 12 $\neq$ 8)
Point (3,9) satisfy the equation y = 2x + 3. (∵ y =2 × 3 + 3 = 9)
Point (4,12) does not satisfy the equation y = 2x + 3. (∵ y = 2 × 4 + 3 = 11 $\neq$ 12)
Point (5,15) does not satisfy the equation y = 2x +3. (∵ y= 2 × 5 + 3 = 13 $\neq$ 15)
Hence, the point (3,9) lies on the line y = 2x +3.

Page No 177:

Question 20:

Which of the following points does not lie on the line y = 3x + 4?
(a) (1, 7)
(b) (2, 0)
(c) (−1, 1)
(d) (4, 12)

Answer:

(d) (4,12)
Explanation:
(a) Point (1,7) satisfy the equation y = 3x + 4. (∵y = 3 × 1 + 4 = 7)
(b) Point (2,10) satisfy the equation y = 3x + 4. (∵y = 3 × 2 + 4 = 10)
(c) Point (-1,1) satisfy the equation y = 3x + 4. (∵y = 3 × -1 + 4 = 1)
(d) Point (4,12) does not satisfy the equation y = 3x + 4. (∵ y = 3 × 4 + 4 = 16 ≠ 12)
Hence, the point (4,12) do not lie on the line y = 3x +4.

Page No 177:

Question 21:

Which of the following points does not lie in any quadrant?
(a) (3, –6)
(b) (–3, 4)
(c) (5, 7)
(d) (0, 3)

Answer:

The point (3, –6) lies in the fourth quadrant.
The point (–3, 4) lies in the second quadrant.
The point (5, 7) lies in the first quadrant.
The point (0, 3) lies on the positive direction of y-axis.
Thus, the point (0, 3) does not lie in any quadrant.
Hence, the correct answer is option (d).

Page No 177:

Question 22:

The area of ∆AOB having vertices A(0, 6), O(0, 0) and B(6, 0) is
(a) 12 sq units
(b) 36 sq units
(c) 18 sq units
(d) 24 sq units

Answer:

The points A(0, 6), O(0, 0) and B(6, 0) can be plotted on the Cartesian plane as follows:
Here, ∆AOB is a right triangle right angled at O.
OA = 6 units and OB = 6 units
∴ Area of ∆AOB = $\frac{1}{2} \times OA \times OB = \frac{1}{2} \times 6 \times 6$ = 18 square units
Hence, the correct answer is option (c).

View NCERT Solutions for all chapters of Class 9

Download RS Aggarwal Chapter 1 Class 9 Maths Exercise 1.6 Solutions

Important Definition for RS Aggarwal Chapter 11 Class 9 Maths Ex 1f Solutions

Related posts:

Page No 174:

Question 1:

Answer:

Page No 175:

Question 2:

Answer:

Page No 175:

Question 3:

Answer:

Page No 175:

Question 4:

Answer:

Page No 175:

Question 5:

Answer:

Page No 175:

Question 6:

Answer:

Page No 175:

Question 7:

Answer:

Page No 176:

Question 1:

Answer:

Page No 176:

Question 2:

Answer:

Page No 176:

Class 9 Rs Aggarwal Chapter 1

Question 3:

Answer:

Page No 176:

Question 4:

Answer:

Page No 176:

Question 5:

Answer:

Page No 176:

Question 6:

Answer:

Page No 176:

Question 7:

Answer:

Page No 176:

Question 8:

Answer:

Page No 176:

Question 9:

Answer:

Page No 177:

Question 10:

Answer:

Page No 177:

Question 11:

Answer:

Page No 177:

Question 12:

Answer:

Page No 177:

Question 13:

Answer:

Class 9 Rs Aggarwal Chapter 15

Page No 177:

Question 14:

Answer:

Page No 177:

Question 15:

Answer:

Page No 177:

Question 16:

Answer:

Class Ix Rs Aggarwal All Chapter Book

Page No 177:

Question 17:

Answer:

Class Ix Rs Aggarwal All Chapter 2

Page No 177: